View Planning

Consider you’re an actor and you are walking around in an open space, go sightseeing, etc. And you have a drone that tracks you in 3D and fly around you, which many of the commercial personal drones are able to do so already. You will have a video out of it recording your movement, and with many state-of-the-art methods, you can reconstruct a 3D model in high fidelity (point cloud or mesh) of yourself from the video. In fact, it is actually 4D since it’s a sequence of your motion in 3D, and your surface is changing over time.

The quality of the 3D reconstruction is highly dependent on the camera motion, i.e., how the drone moves around you. And the question is, how should the drone move around you to maximize the quality of the 3D reconstruction?

Note that there are two main difficulties here:

1. The surface of the actor is changing over time, and therefore we cannot use what we’ve observed in the past to reconstruct the present.
2. Similarly, because of the changing surface, also because the reconstruction algorithm is computationally expensive and can not be run in real-time (during the flight), there is no closed-form objective function that we can optimize for the drone’s trajectory. The traditional ‘Next Best View’ (NBV) methods are not applicable here.

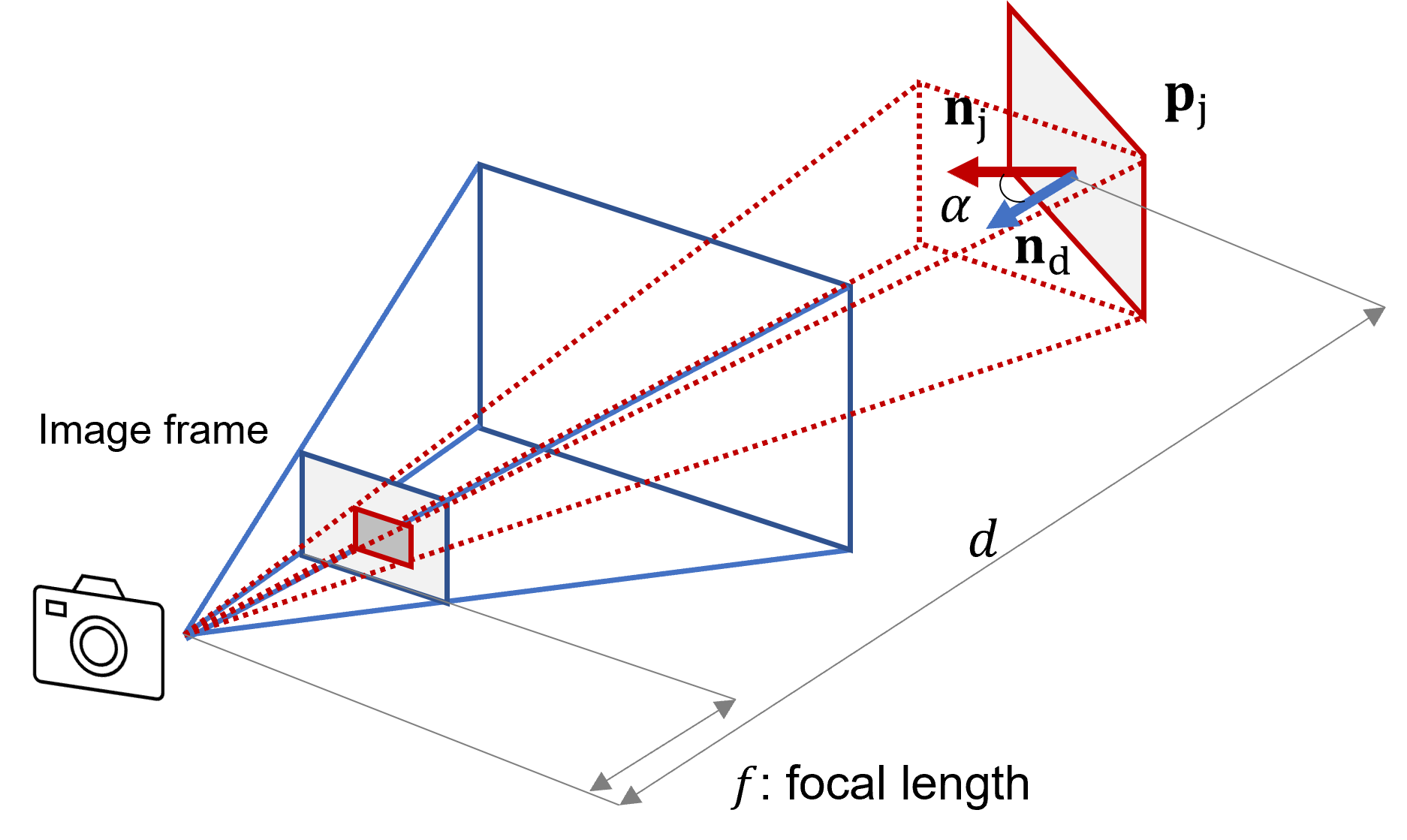
Therefore, let’s consider a simpler problem first. Let’s consider a single static 3D patch $\mathbf{x}_j$, indexed by $j$, centered at $\mathbf{p}_j$, with a surface normal $\mathbf{n}_j$. It can be any 3D primitive, such as a triangle from a mesh. Now let’s measure how well we are observing this patch from a 6D drone (camera) pose $\mathbf{x}_d = (\mathbf{p}_d, \mathbf{n}_d)$.

Pixels-Per-Area (PPA)

To define the quality of the observation of a camera pose to a single 3D patch, we propose a new metric called Pixels-Per-Area (PPA). PPA defines the projected area of the 3D patch in the image plane, divided by its actual area in 3D space.